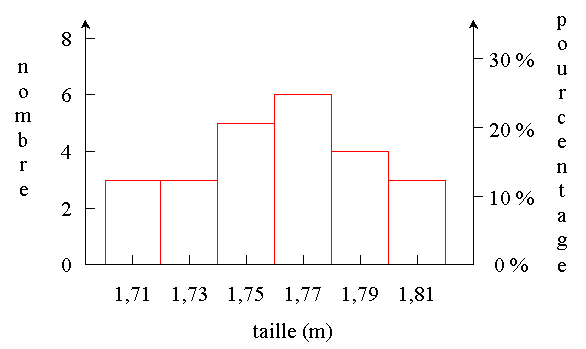
Les classes sont généralement repérées par leur
centre, mais elles doivent être définies
par leurs extrémités.
3. Choix de la largeur des classes
La largeur choisie pour les classes dépendra:
-
de la finesse de la représentation désirée
(si on veut faire la distinction entre des individus dont la taille
diffère de 5 cm, on ne va pas choisir des classes plus larges, par
exemple 10 cm!)
-
de la taille de l'échantillon étudié
Pour que la représentation ait suffisamment de précision, il faut que
chaque classe contienne, en général, un nombre suffisant d'individus.
Exemple:
Les cotes obtenues à un examen par 50 élèves sont données dans le tableau
suivant:
0.0
0.0
0.5
1.2
1.7 |
2.1
3.2
4.5
5.3
5.3 |
6.1
6.2
7.2
7.2
7.4 |
7.8
8.2
9.1
9.1
9.5 |
9.5
9.6
9.9
9.9
10.1 |
10.4
10.5
11.1
11.8
11.9 |
12.1
12.4
12.5
12.6
12.6 |
12.8
12.8
12.9
13.0
13.7 |
13.9
14.2
14.6
14.7
14.7 |
14.8
15.5
16.1
16.8
18.2 |
|
Choisissez la largeur des classes et examinez son effet sur l'allure de
l'histogramme:
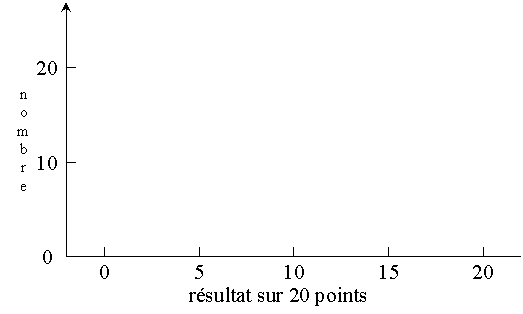
Largeur des classes:
1
2
4
5
10
toutes les classes
4. Polygone des fréquences ou des effectifs
Pour obtenir ce polygone, on raccorde les sommets des barres, au centre de
chaque classe, par des segments de droite.
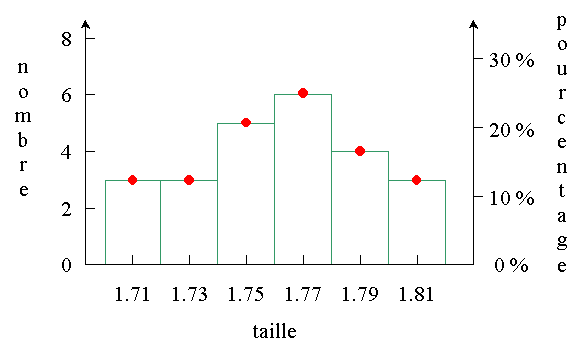
On obtient donc une série de points reliés par des segments de droite.
L'abscisse de chaque point
correspond au centre de la classe. La hauteur
de chaque point (son ordonnée) correspond au
nombre d'individus dans la classe
(polygone des effectifs) ou au
pourcentage d'individus dans la classe
(polygone des fréquences).
5. Bien interpréter les graphes
Il est courant d'entendre déclarer que l'on fait dire aux statistiques
ce que l'on veut. Par exemple, il est possible de présenter les résultats
de manière à amener le lecteur peu attentif à accepter une conclusion
erronée.
Le but de ce chapitre est d'illustrer cette pratique par quelques exemples,
afin de vous aider à interprèter correctement les graphes parfois
trompeurs.
Cas étudiés:
|
1. Tirage de journaux concurrents

|
Le graphique suivant est paru en 1981 dans le
New Yorker Post, sous le titre
"Ascension du Post, le quotidien préféré des
New-Yorkais".
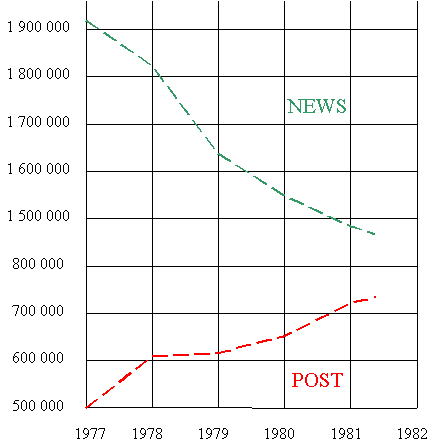
Le but de ce graphique est de convaincre le lecteur que la croissance du
tirage du Post va bientôt l'amener
en première position, devant le News, qui
périclite.
On remarque deux artifices utilisés pour exagérer la tendance:
-
L'échelle verticale ne démarre pas en zéro.
C'est une présentation acceptable, mais qui renforce les variations
apparentes.
-
L'échelle verticale est discontinue.
Alors que deux graduations successives sont séparées de 100.000 unités,
on passe brutalement de 800.000 à 1.500.000 dans l'intervalle séparant le
POST du NEWS. Les tirages des deux journaux paraissent, de ce fait,
beaucoup plus proches que dans la réalité.
Une telle
présentation ne serait
admissible que si la discontinuité de l'échelle était clairement
indiquée, par exemple par des pointillés:
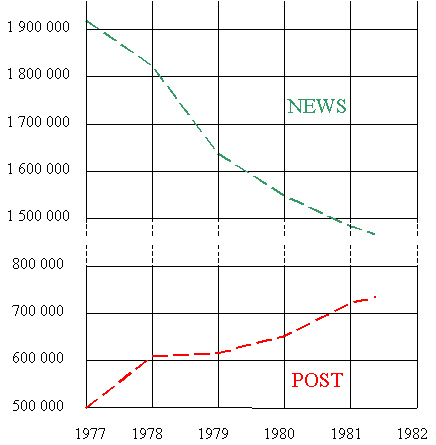
La version correcte, plus "honnête",
du graphique, est la suivante:
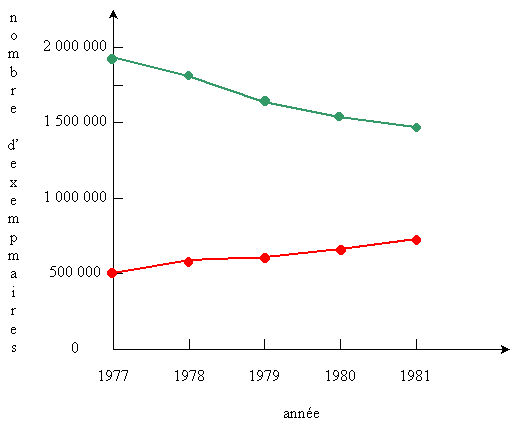
On constate immédiatement qu'il reste au Post
bien du chemin à parcourir avant d'accéder à la première place.
|
2. Le baril de pétrole
géant

|
La figure de gauche, parue dans le magazine
Time du 9 avril 1979, est destinée à illustrer
l'augmentation du prix du pétrole suite à la crise déclenchée par la guerre
du Kippour.
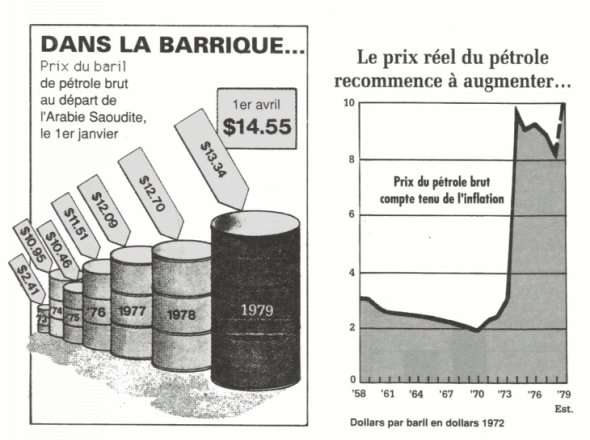
De 1973 à1979, le prix du pétrole a été multiplié par 6. Or, le baril
"1979", qui est 6 fois plus haut que le baril "1973" contient
6×6×6 = 216 fois plus de
pétrole que celui-ci
Ce n'est pas la hauteur du baril, mais son volume, que le lecteur associera
généralement au prix (le pétrole se vend au litre,
pas au mètre !)
On a donc exagéré d'un facteur 36
l'augmentation du prix du pétrole.
Si, de plus, on tient compte de l'inflation (figure de droite), le prix du
pétrole n'a augmenté que d'un facteur 3,5
entre 1973 et 1979.
L'exagération est de 60 fois !
|
3. Dépenses gouvernementales aux
Etats-Unis

|
Le graphique de gauche illustre l'accroissement des dépenses
gouvernementales US de 1930 à 1980. On constate une augmentation régulière
si on mesure ces dépenses en dollars, avec un
petit pic correspondant à la seconde guerre mondiale.
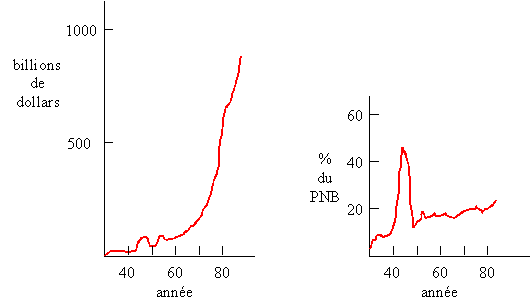
Cependant, la mesure des dépenses en dollars n'a pas beaucoup de sens car
elle ne tient pas compte de l'inflation.
Ce qui est plus significatif dans ce cas, c'est l'évolution des dépenses
gouvernementales par rapport à toutes les autres dépenses, mesurées ici par
le Produit National Brut (PNB).
|
4. Production alimentaire mondiale

|
Le graphe suivant, publié dans l'hebdomadaire
Business Week le 16 juin 1975, est destiné à
illustrer la variation de la production alimentaire, comparée à celle de la
population mondiale.
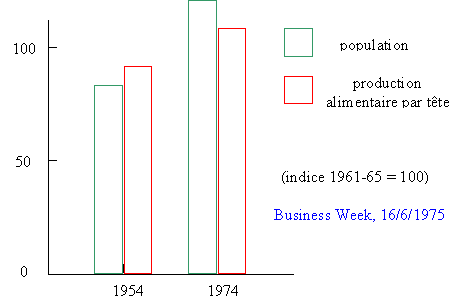
La plupart des personnes examinant ce graphe vont conclure que la
production alimentaire a augmenté moins vite
que la population. Le piège réside dans le fait de comparer la production
alimentaire par tête (=par individu) à
la population totale. Si la production
alimentaire par tête augmente, cela
signifie forcément que la production totale augmente plus vite que la
population totale.
Une version plus claire de ce graphe est présentée ci-dessous:
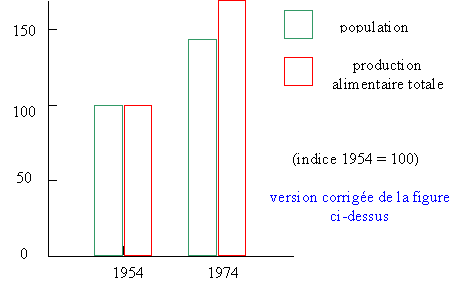
NB: Il faut bien se garder d'interprèter les
graphe au-delà de ce qu'ils
présentent. Du graphe ci-dessus, on ne peut pas déduire, par exemple, que
le problème de la faim dans le monde était moins aigu en 1974 qu'en 1954.
En effet, ce problème dépend de bien d'autres facteurs, comme la
répartition des denrées alimentaires entre pays et entre couches de la
population.
|
5. Le camembert en perspective

|
Le diagramme sectoriel suivant présente les pourcentages obtenus par 4
partis politiques lors d'une élection.
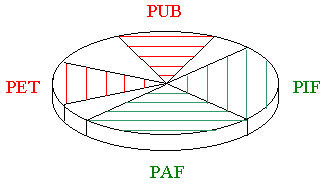
Exercice: Sur base de ce graphe,
indiquez lequel de ces
4 partis a obtenu le plus de suffrages et lequel en a obtenu le
moins ?
|
6. Choix de l'année de base

|
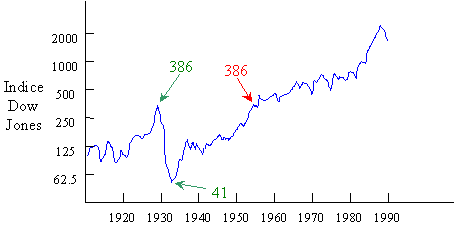
L'évolution du marché boursier à Wall Street avant 1954 est illustrée sur
le graphiques ci-dessous:
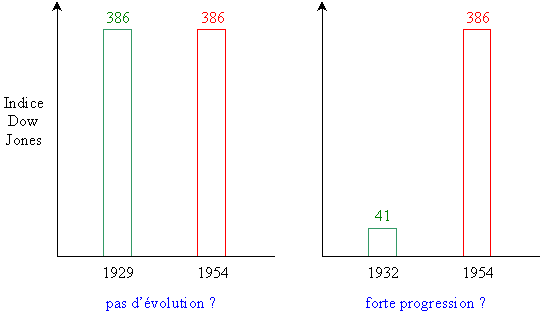
En regardant le graphe de gauche, on a l'impression que l'indice Dow Jones
n'a pas évolué. Par contre, le graphe de
droite suggère une forte progression.
Ces deux graphiques, trop schématiques, donnent une vue tronquée de
l'évolution du marché boursier. En examinant l'évolution complète de
celui-ci, on constate que les années 1929 et 1932 prise comme références
correspondent en fait à un pic et un creux de la courbe, la grande crise de
1930 ayant provoqué l'effondrement du cours des actions.
6. Echelle logarithmique
Lorsque la grandeur à représenter varie fortement (p.ex., plus d'un facteur
100), l'échelle habituelle (linéaire) n'est pas bien adaptée à la
représentation des petites quantités.
Exemple: Les dimensions caractéristiques des
objets suivants sont:
mouche:
homme:
terrain
de football:
village:
pays:
planète terre: |
5 mm = 0.005 m
2 m
100 m
1 km = 1000 m
1000 km = 1 000 000 m
12 000 = 12 000 000 m |
Représentation linéaire
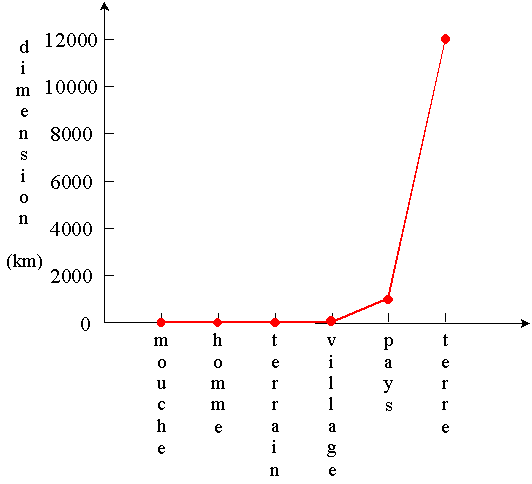
Dans une représentation linéaire, où une
longueur donnée (entre deux graduations successives) correspond à
l'addition d'une quantité fixée (p.ex.,
2000 km), les petites variations sont indiscernables. Ainsi, le
graphique ci-dessus ne permet pas de distinguer la dimension d'une mouche
de celle d'un terrain de football.
Dans la représentation logarithmique, une
longueur fixe (entre deux graduations successives) correspond à la
multiplication par un nombre donné (p.ex.,
100).
Représentation logarithmique
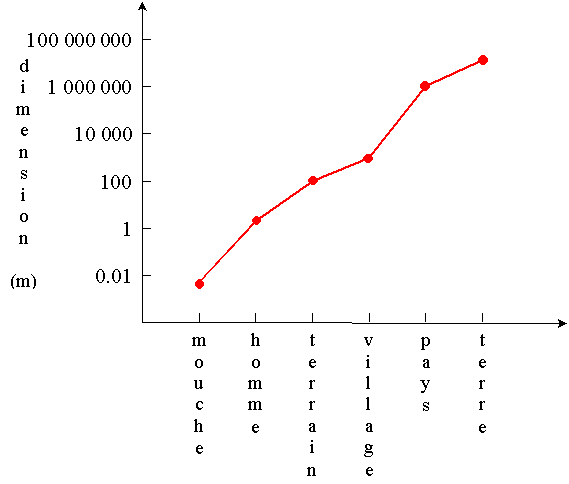
7. Evolution temporelle d'une grandeur
Une utilisation courante de la (des)
statistique(s) concerne l'étude de la
variation d'une quantité quelconque au cours du temps (chiffre d'affaires
d'une société, prix d'une denrée, produit national brut, audience d'une
chaîne de télévision,...)
Exemple: on étudie le nombre annuel de décès
dans une paroisse ardennaise (Rahier) vers la fin du XVIIIe
siècle en dépouillant les registres paroissiaux. Cette étude donne les
résultats suivants:
1766:
1767:
1768:
1769:
1770:
1771:
1772:
1773:
1774:
1775: |
13 décès
13 décès
10
décès
6 décès
10 décès
14
décès
10 décès
21 décès
17 décès
6 décès |
Le nombre total de décès sur cette période de 10 ans est de
120, soit une moyenne de
12 décès par an, ou encore
1 décès par mois.
L'histogramme et le polygone des effectifs sont présentés ci-dessous:
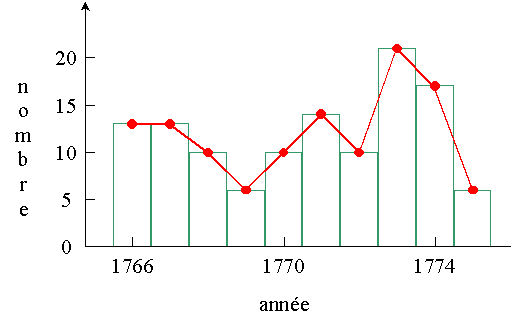
On se pose alors la question suivante:
Y-a-t'il une année pour laquelle le nombre de décès
est anormalement faible ou élevé ?
La Théorie nous enseigne que si le nombre
moyen de décès est de 12 par an, on peut
s'attendre, chaque année, à un nombre de décès variant de
5 à 19, avec un
intervalle de confiance de 95 %.
Autrement dit, les fluctuations statistiques vont,
normalement (dans 19 cas sur 20) faire varier
le nombre de décès de 5 à
19 chaque année.
Une seule année sort de cet intervalle: 1773, avec
21 décès.
Cette différence est-elle significative ?
(Après tout, 1 fois sur 20, on s'attend à un nombre de décès inférieur à
5 ou supérieur à
19)
Examinons les données en détail.
Pour 1766, une année "moyenne"
(13 décès),
le prêtre a consigné dans son registre les décès suivants:
-
le 5 janvier, Jeanne, fille de Mathieu Pichay
-
le 9 janvier, Bartholomé, fils de Bartholomé Caporal
-
le 22 janvier, Catherine Capon, épouse de François Boutet
-
le 27 janvier, Jean Henri Cola
-
le 11 février, un enfant de Mathieu Collinet
-
le 23 avril, Pierre Calais
-
le 10 mai, Marie Joseph Sauvage, veuve de Jean Boutet
-
le 14 mai, Jean Joseph, fils de Joseph Grégoire
-
le 18 juin, Marie Piette, veuve de Joseph Xhardé
-
le 20 novembre, Martine N., mendiante
-
le 4 décembre, Toussaint Charrette
-
le 8 décembre, Marie Jeanne Helman; épouse de Gilles Lerus
-
le 27 décembre, Aubin Jacquet
Soient 9 adultes, 4 enfants
Pour 1776, le registre porte les 21 décès
suivants:
-
le 13 janvier, Catherine, fille de Joseph Malhache
-
le 26 janvier, Marie Anne Donneau; veuve de Joseph Chauveheid
-
le 13 février, Jean Helman
-
le 27 février, Marie Jeanne Quenech, veuve de Jean Helman
-
le 28 mars, Elisabeth Marly, épouse de Servais Rasquin
-
le 15 avril, un enfant de Querin Chauveheid
-
le 17 avril, Anne Marie Charette, épouse de Henri Jacquemin
-
le 18 avril, un enfant de Querin chauveheid
-
le 22 avril, un enfant de Pierre Jacquet
-
le 23 avril, un enfant, veveu de Mathieu Deroanne
-
le 24 avril, un enfant de Henri Goffin
-
le 26 avril, un enfant de Jean François Reharmont
-
le 8 mai, un enfant de Louis Dorquet
-
le 16 mai, Anne Marie, fille de Jean François Deroanne
-
le 2 juin, un enfant de François Santkin
-
le 7 juin, Jacques Laffru
-
le 18 juin, Mathieu, fils de Jean Debatty
-
le 21 juin, un enfant de Guillaume Smettre
-
le 4 juillet, une enfant de Louis Dorquet
-
le 14 novemvre, un enfant de Jean Pierre Boutet
-
le 14 décembre, Marie Ursule Deremouchamps, épouse de Henri Neuforge
Soient 7 adultes, 14 enfants
En particulier, on relève 14 décès entre le 15
avril et le 4 juillet, dont 10 enfants.
soient 5 décès/mois au lieu de 1
Entre le 15 avril et le 26 avril, on note 7
décès, dont 6 enfants
soient 20 décès/mois au lieu de 1
Ces indices sont suffisants pour conclure à une épidémie touchant surtout
les enfants, par exemple: dysenterie
L'examen détaillé des données a donc confirmé la
conclusion théorique.
Chapitre:
1
2
3
4
5
6
7





