|
1. Ecart type pour les proportions
Considérons le cas d'un sondage politique.
Ici, on ne désire plus estimer la moyenne d'une grandeur sur une
population, mais la proportion des individus de cette population qui se
rangent dans une catégorie (p.ex., qui déclarent voter pour le P.U.B.).
Exemple:
Un institut de sondage interroge un échantillon
représentif de 200 électeurs, qui ont le choix entre 4 partis
politiques.
Les résultats du sondage sont les suivants:
|
parti
|
nombre d'intentions de vote
| |
PUB
PET
PAF
PIF
ne se prononcent
pas
|
24
35
69
61
11
|
Notons p la proportion d'individus d'une
classe dans l'échantillon.
Si n1 est le nombre d'individus
dans la classe 1 et n le nombre total
d'individus dans l'échantillon, on a:
et de même
Dans notre sondage, les proportions sont les
suivantes:
|
parti
|
proportion
| |
PUB
PET
PAF
PIF
n.s.p.
|
0,120
0,175
0,345
0,305
0,055
|
Si l'échantillon est représentatif, la proportion
p dans l'échantillon est une approximation de
la proportion  dans la population. dans la population.
Pour des échantillons suffisamment grands, les
proportions suivent une loi normale, avec un écart type d'échantillon
de:
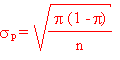
En général, la proportion  dans la population
n'est pas connue. On la remplace alors par la proportion
p dans
l'échantillon dans la population
n'est pas connue. On la remplace alors par la proportion
p dans
l'échantillon
Les proportions obéissent à des lois comparables à
celles des moyennes.
Une différence importante est que l'écart type
peut être calculé à partir des proportions
(pour les moyennes, il devait être connu par
ailleurs).
Nous pouvons donc calculer les intervalles de confiance à 95 % sur les
intentions de vote:
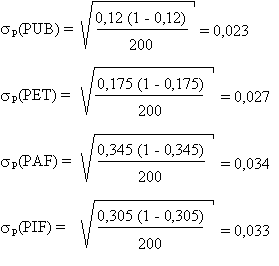
Les intervalles de confiance à 95 % sont de
2 P P
Les résultats du sondage sont les suivantes:
|
parti
|
intentions de vote
| |
PUB
PET
PAF
PIF
|
12,0 ± 4,6 %
17,5 ± 5,4 %
34,5 ± 6,8 %
30,5 ± 6,6 %
|
2. Les proportions sont des moyennes
Considérons une élection opposant deux partis A et B
Considérons la grandeur x = nombre de voix qu'un
électeur apporte au parti B.
C'est une variable discrète qui peut prendre deux valeurs:
|
x = 0
|
si l'électeur vote pour A
| |
x = 1
|
si l'électeur vote pour B
|
Soient:
|
nA
|
le nombre d'électeurs votant pour A
| |
nB
|
le nombre d'électeurs votant pour B
| |
n
|
le nombre total d'électeurs
| |
p
|
la proportion d'électeurs votant pour B
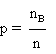
|
Calculons la valeur moyenne de x:
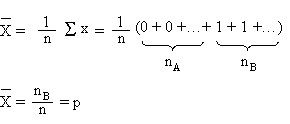
La proportion est donc la moyenne de x
Calculons l'écart type sur x (ou plutôt son carré, appelé
variance)
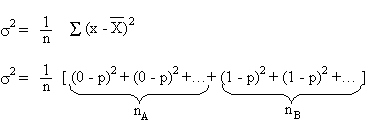
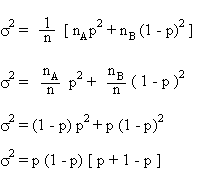
On a donc
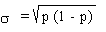
Et donc,
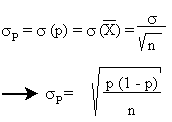
3. Exemples
EXEMPLE 1:
Afin de prédire le résultat d'une élection opposant deux partis, on
interroge un échantillon représentatif de 100 électeurs. 60 déclarent voter
pour le parti 1 et 40 pour le parti 2.
Quelle est la probabilité que le parti 1 gagne
les élections ?
Solution:
On ne peut pas calculer:
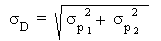
car les 2 échantillons ne sont pas indépendants !
Le parti 1 gagne les élections si p1 > 0,5
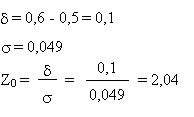
table 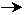 Prob = 0,021 Prob = 0,021
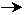 il y a 2,1 % de chances que
p1 < 0,5 il y a 2,1 % de chances que
p1 < 0,5
 il y a 100-2,1 = 97,9 % de chances
que le parti 1 remporte les élections il y a 100-2,1 = 97,9 % de chances
que le parti 1 remporte les élections
EXEMPLE 2:
On constate un défaut dans 20 % des voitures d'un modèle. Un garagiste,
qui a vendu 50 voitures de ce modèle, fait revenir tous ses clients afin de
remplacer une pièce aux voitures défectueuses. Pour cela, il a commandé 12
pièces de rechange.
Quelle est la probabilité qu'il n'ait pas suffisamment
de pièces?
Solution:
La proportion de voitures défectueuses vaut
 = 0,2. = 0,2.
Dans l'échantillon de 50 voitures, on s'attend à la même proportion,
avec un écart type:
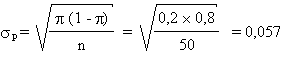
Il n'aura pas suffisamment de pièces si le nombre de voitures défectueuses
est supérieur à 12, ou au moins égal à 13.
On a le choix entre deux critères:
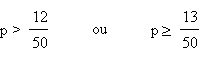
Dans ce cas, on obtient un meilleur résultat en appliquant la
correction de continuité et en choisissant
12,5 plutôt que 12 ou 13.
Nous retiendrons donc
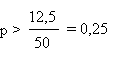
Pour qu'il n'ait pas assez de pièces de rechange, il faut donc que la
proportion s'écarte de la valeur moyenne de plus de
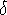 = 0,25 - 0,2 = 0,05 = 0,25 - 0,2 = 0,05
On obtient donc:
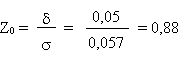
La probabilité d'avoir un écart au moins aussi élevé est, d'après la table
de la loi normale, de 0,189.
Il y a donc 18,9 % de risques que le garagiste n'ait pas assez de
pièces de rechange.
4. Illustration: test de la fiabilité des horoscopes
Lors de deux leçons, nous organisons un test destiné à mesurer la fiabilité
des horoscopes.
Dans ce but, nous distribuons des feuilles reprenant les horoscopes de la
semaine précédente.
Chaque étudiant présent lit ces horoscopes et indique:
Pour le premier test, les signes astrologiques sont indiqués.
Dans le second test, ces signes ne sont pas indiqués et l'ordre en est
modifié.
Ce test a pour but de répondre à deux questions:
Nous désignerons par "coïncidences
positives" (CP) les cas où l'étudiant a reconnu son signe,
c'est-à-dire les cas où l'horoscope qu'il a sélectionné correspond bien à
son signe.
Les résultats des deux tests effectués de 1998 à 2008 sont résumés dans ce
tableau suivant:
année |
signes connus |
signes inconnus |
n |
CP |
n |
CP |
1998-2001
2002
2003
2004
2007
2008
|
145
71
57
81
61
55
|
46
9
10
15
12
6
|
275
71
72
44
58
64
|
22
9
5
2
6
5
|
total |
470 |
9 |
584 |
49 |
1. Test de la fiabilité des
horoscopes
Nous considérons l'ensemble des quatre
années et retenons les tests où les signes n'étaient pas
connus, afin d'éviter des biais éventuels
Nous avons un échantillon de 584 réponses, avec 49 coïncidences
positives
Si ces coïncidences positives étaient
dues au hasard
uniquement, c'est-à-dire si chaque individu répondait au hasard, il aurait
une chance sur 12 de choisir l'horoscope correcpondant à son signe.
Par le hasard seul, nous nous attendrions donc à:
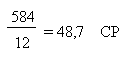
Or, nous avons 49 CP, ce qui est pratiquement égal au nombre
attendu par l'action du hasard.
C'est très mauvais signe pour la fiabilité des
horoscopes !
Nous allons cependant utiliser nos connaissances en statistique pour
analyser ces tests de manière plus quantitative.
(a) le nombre de coïncidences positives est
compatible avec l'action du hasard seul.
Dans le cas d'une répartition au hasard, le nombre de CP doit être,
en moyenne, 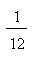 du nombre de
réponses. du nombre de
réponses.
La proportion de CP, p+, vaut donc:
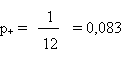
avec un écart type
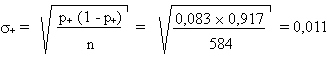
L'intervalle de confiance à 95 % vaut donc:
0,083 ± 0,022
ou encore:
[0,061;0,105]
La valeur obtenue par l'étude de notre échantillon vaut:
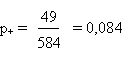
Elle se trouve dans l'intervalle de confiance pour une répartition due au
hasard.
On peut donc conclure que la petite différence entre la valeur mesurée et la
valeur attendue est parfaitement compatible avec le hasard: c'est ce qu'on
appelle une fluctuation statistique.
Exemple de fluctuation statistique
Si on lance une pièce de monnaie, on s'attend à avoir, en moyenne, autant
de "pile" que de "face".
Sur 100 lancers, on s'aura que rarement 50 "pile" et 50 "face" exactement.
Les écarts par rapport à ce nombre moyen sont les fluctuations
statistiques.
|
ex:
| 47 pile et 53 face,
52 pile et 48
face,
...
|
(b) Avec quelle confiance pouvons-nous conclure à la
non-fiabilité des horoscopes ?
Nous devons tout d'abord définir ce que nous entendons par fiabilité des
horoscopes.
Si l'astrologie était une science exacte, elle devrait être capable
de prédire avec certitude ce qui va nous arriver.
Toutefois, nous ne lui en demonderons pas tant.
Nous dirons que les horoscopes sont fiables à 50 % si les prédictions
concernant notre signe sont celles qui correspondent le mieux à ce qui nous
arrive, dans au moins un cas sur deux.
Dans ce cas, au moins la moitié des individus
devraient reconnaître leur signe.
Remarque: cette définition est très peu contraignante pour
l'astrologie. En effet:
-
Nous ne lui demandons pas de prédire avec précision ce qui va nous
arriver, mais seulement que la prédiction concernant notre signe soit la
plus proche de ce qui va nous arriver, parmi les 12 prédictions;
-
nous ne demandons pas que cela se produise pour tous les individus, mais
seulement pour la moitié d'entre eux.
Soit p+ la proportion des individus qui reconnaissent leur
signe.
Dans notre échantillon, nous avons:
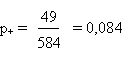
avec un écart type:
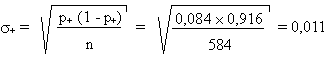
Pour que les horoscopes soient fiables à 50 %, il faudrait, dans la
population, une proportion p+  0,5, donc un écart minimum avec notre valeur
d'échantillon: 0,5, donc un écart minimum avec notre valeur
d'échantillon:
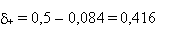
et donc
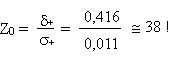
Cette valeur est si grande qu'elle ne figure pas dans notre table de la
loi normale.
En fait:
Il n'y a pas une chance sur des millards de milliards
pour que les horoscopes testés soient fiables à 50 %
Notre échantillon nous permet d'exclure cette
hypothèse avec une certitude quasi absolue.
Les horoscopes pourraient-ils être fiables à
25 % ?
Pourrait-il y avoir une chance sur 4 pour que la prédiction qui correspond
le mieux à un individu soit celle de son signe ?
Dans ce cas, au moins un quart des individus devraient reconnaître
leur signe.
Il faudrait donc p+  0,25,
et donc un écart 0,25,
et donc un écart
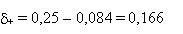
et:
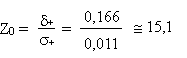
Cette valeur est, une fois de plus, en dehors de la table de la loi
normale.
Notre test nous permet d'exclure avec une quasi
certitude que les horoscopes testés soient fiables une fois sur
4.
Tester une fiabilité plus faible n'a pas beaucoup de
sens car:
-
être fiable moins d'une fois sur 4, c'est plutôt être
non fiable.
-
le hasard seul donne une fiabilité d'une fois sur 12
 on risque évidemment de
trouver que les horoscopes sont fiables une fois sur 12 ! on risque évidemment de
trouver que les horoscopes sont fiables une fois sur 12 !
En résumé:
Nous pouvons conclure que la fiabilité des horoscopes testés est nulle,
puisque l'on obtiendrait le même résultat en choisissant les signes
au hasard.
Si vous lisez les horoscopes, rien ne sert de connaître votre signe.
Les prévisions des autres signes s'appliquent tout aussi bien (ou
plutôt: tout aussi mal) à vous !
2. La connaissance du signe a-t-elle influencé
les réponses ?
Nous allons tâcher de déterminer si les individus testés se sont
laissé influencer par la connaissance de leur signe, lorsque celui-ci était
indiqué.
Dans les tests avec signes connus, nous avons 79 coïcidences positives
sur 470 réponses , soit une proportion
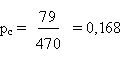
avec un écart type:
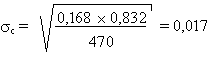
Avec les signes inconnus, nous avons 49 coïcidences positives sur 584
réponses, soit une proportion
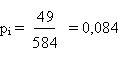
avec un écart type:
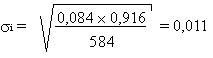
On a donc une proportion plus grande de coï:ncidences positives lorsque
les signes sont connus, ce qui laisse supposer que certains individus se
sont laissé influencer par la connaissance de leur signe.
Cette différence est-elle statistiquement
significative ?
Avec quelle confiance pouvons-nous affirmer que cette différence ne peut
pas être due à l'action du hasard (fluctuation statistique).
Nous pouvons supposer que les deux échantillons sont indépendants car nous
ne voyons pas comment la réponse à un des tests pourrait influencer la
réponse à l'autre.
Nous avons une différence de proportion
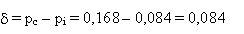
entre les CP avec signes connus et inconnus.
L'écart type sur cette différence vaut:
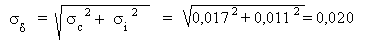
Nous obtenons donc
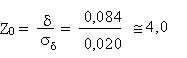
D'après la loi normale, la probabilité qu'un tel écart soit dû au
hasard est de 0,00003 = 0,003%.
Nous pouvons donc conclure avec 99,997 % de confiance que la
connaissance du signe a effectivement influencé les réponses.
Ce résultat illustre l'importance de réaliser les tests "à l'aveugle", sans
que les sujets testés puissent se laisser influencer par la connaissance
d'informations de nature à influencer le résultat. Même en essayant
de ne pas tenir compte de ces informations, on risque fort de se laisser
influencer.
Chapitre:
1
2
3
4
5
6
7
|





