|
1. Echantillons représentatifs et échantillons biaisés
Le but principal de la statistique est de déterminer les caractéristiques
d'une population donnée à partir de l'étude
d'une partie de cette population, appelée échantillon.
 |
La façon de sélectionner
l'échantilon est aussi
importante que la manière de l'analyser. |
 |
Il faut que l'échantillon soit représentatif
de la population.
L'échantillonnage aléatoire est le meilleur moyen
d'y parvenir.
Un échantillon aléatoire est un échantillon
tiré au hasard dans lequel tous les individus
ont la même chance de se retrouver.
Dans le cas contraire, l'échantillon est biaisé.
Un petit échantillon représentatif est, de loin, préférable à un grand
échantillon biaisé.
Exemple:
Nous désirons déterminer la taille moyenne des étudiants de 2e
candi. Commu. (97-98) qui étaient présents au 1er cours
de statistique, à partir d'un échantillon de 10 individus.
(la réponse exacte, pour la population totale de 86
étudiants, est de 174,0 cm).
Mus par une bonne intention, sachant que les garçons sont, en général, plus
grands que les filles, nous choisissons un échantillon contenant autant de
filles que de garçons.
Soient 5 filles et 5 garçons choisis au hasard:
Taille des filles
(cm) |
Taille des garçons
(cm) |
171
165
173
174
166 |
193
187
180
185
178 |
A partir de cet échantillon de 10 individus, nous obtenons une taille
moyenne de 177,2 cm, soit
3,2 cm
de plus que la valeur exacte.
Avons-nous procédé correctement au choix de
l'échantillon, sachant que la population contient 51 filles et 35
garçons ?
Non, car chaque garçon avait plus de chances
d'être choisi que chaque fille.
En effet, les 5 garçons étant tirés au hasard dans une population de
35 individus, chacun d'eux avait 5 chances sur 35 d'être choisi,
soit une probabilité de 5/35  0.143. 0.143.
Les 5 filles étant choisies dans une population de 51 individus, chacune
d'entre elles avait 5 chances sur 51 d'être choisie, soit une probabilité
de 5/51  0.098, donc nettement plus faible que
pour les garçons. 0.098, donc nettement plus faible que
pour les garçons.
Nous avons biaisé l'échantillon en faveur des garçons. Il n'est donc pas
surprenant que nous obtenions un résultat trop élevé.
La manière correcte de procéder est de choisir au hasard dans toute la
population, sans considération du sexe.
Un tel tirage au hasard a donné les tailles suivante (en
cm): 187,165,180,168,165,160,174,183,168,176
La moyenne de l'échantillon est de 172,6 cm
Elle est plus proche de la valeur exacte (erreur de -1,4 cm au lieu de
+3,2 cm)
[En fait, vu les petits échantillons utilisés, le hasard
aurait pu donner un résultat inverse. Ce sera beaucoup moins probable pour
de grands échantillons. Le raisonnement est néanmoins valable en toute
généralité.]
Une autre manière de procéder est d'utiliser la technique des
quotas.
Sachant que la population édudiée contient 35/86  40 % de garçons et 51/86
40 % de garçons et 51/86  60 % de
filles, nous pourrions nous assurer que l'échantillon respecte les même
proportions, soit 4 garçons et
6 filles. 60 % de
filles, nous pourrions nous assurer que l'échantillon respecte les même
proportions, soit 4 garçons et
6 filles.
Exercice:
Les échantillons suivants sont-ils représentatifs de la population visée ?
-
Pour connaître les opinions politiques de la population d'une ville,
on envoie 5 enquêteurs interroger les gens à la sortie de 5 grands
magasins. Ils doivent questionner les clients jusqu'à ce qu'ils réunissent,
chacun, un échantillon de 200 réponses.
-
On désire faire une enquête sur les goûts musicaux de la
population belge.
Pour cela, on choisit au hasard 1000 numéros de téléphone
dans l'ensemble des annuaires et on les appelle pendant les heures de
bureau. On obtient 583 réponses.
Ces exemples illustrent la difficulté de réunir un
échantillon représentatif, surtout lorsqu'il s'agit d'êtres humains
(certains sont plus faciles à joindre, d'autres refusent de
répondre,...)
-
Pour me faire une idée du niveau de la classe, je prends les étudiants des 2
premières rangées et je les questionne. Est-ce un échantillon
représentatif ?
2. Centre d'une distribution
Nous supposons maintenant que notre échantillon est représentatif de la
population.
La moyenne sur l'échantillon et donc une é
estimation de la moyenne sur la population.
Nous désirons savoir quelle est la
précision de cette estimation, afin de
connaître de quelle quantité la vraie valeur est susceptible de
s'écarter de notre estimation.
En fait, la précision va dépendre:
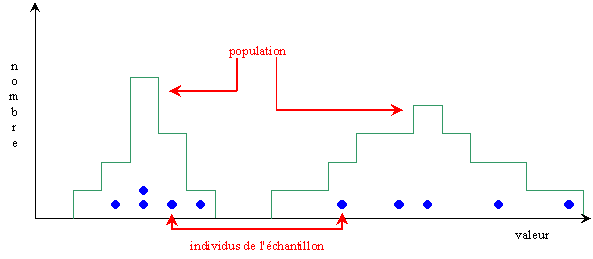
Dans une population peu dispersée, toutes les valeurs de l'échantillon
seront forcément proches de la moyenne.
Dans une population plus dispersée, les valeurs de l'échantillon seront
généralement plus éloignées de la moyenne.
La moyenne de l'échantillon pourra donc s'écarter
plus fortement de celle de la population.
Soient:
Alors, la précision de la moyenne peut être mesurée par un écart type
sur la moyenne:
La précision sur la valeur moyenne sera donc d'autant meilleure que:
La présence d'une racine carrée au dénominateur implique que:
-
pour une précision 2 fois meilleure, il faut un
échantillon 4 fois plus grand.
-
pour une précision 10 fois meilleure, il faut un
échantillon 100 fois plus grand.
 La
précision coûte cher ! La
précision coûte cher !
Exemple:
-
Dans la population de 51 filles de 2e candi. communication,
la taille moyenne est de
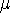 = 167,9 cm = 167,9 cm
(nous noterons
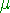 la valeur moyenne - généralement inconnue - pour la population et
la valeur moyenne - généralement inconnue - pour la population et
 la valeur moyenne pour
l'échantillon) la valeur moyenne pour
l'échantillon)
L'écart type sur la taille est de
 = 5,3 cm = 5,3 cm
Si on estime la taille moyenne à partir d'un échantillon de 4 personnes,
on aura une précision (écart type) sur la moyenne de
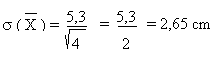
A partir d'un échantillon de 10 personnes, l'écart type serait de:
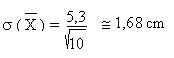
-
Nous désirons déterminer la taille moyenne des hommes belges âgés
d'une vingtaine d'années.
Nous disposons d'un échantillon de 35 étudiants de 2e candi.
communication.
Si cet échantillon est représentatif, sa taille moyenne est une
estimation de celle de la population en question.
Elle est de 182,9 cm
Pour estimer la précision de cette moyenne, il faudrait connaître
l'écart type de la taille pour toute la population considérée, ce qui
n'est pas le cas.
Si notre échantillon n'est pas trop petit
(en principe, au moins 100 individus),
nous pouvons remplacer l'écart type  de la population par l'écart type s
de l'échantillon.
de la population par l'écart type s
de l'échantillon.
Dans ce cas, il vaut:
s = 6,7 cm
La précision sur la moyenne serait donc de:
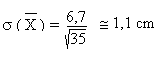
Comme pour la moyenne, nous réserverons les lettres grecques pour les
grandeurs relatives à la population et les
caractères romains pour les grandeurs correspondant à
l'échantillon.
| |
moyenne |
écart type |
population: |
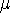 |
 |
échantillon: |
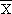 |
s |
Ecart type de la moyenne:
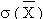
Si l'écart type de la grandeur analysée dans la population n'est pas connu,
on peut le remplacer par l'écart type calculé dans l'échantillon,
pour autant que cet échantillon soit suffisamment
grand.
3. Un exemple d'échantillonnage statistique: l'audimat
Une application courante des sondages statistiques est l'estimation
de l'audimat des émissions de télévision. Nous allons passer en revue
quelques-unes des méthodes utilisées, en présentant leurs principaux
avantages et inconvénients.
Cet exemple illustre bien les difficultés auxquelles on peut parfois
se heurter pour réunir un échantillon représentatif, permettant de
mesurer la grandeur effectivement recherchée.
-
Analyse du courrier
Méthode peu coûteuse
Défaut:
l'échantillon de personnes qui écrivent aux stations n'est pas
représentatif.
-
Interviews
On questionne les gens pour connaître les programmes qu'ils ont
regardé la veille
Défauts:
-
Panels avec journaux d'écoute
Ce sont des groupes permanents de personnes chargées de noter leurs
écoutes et leurs appréciations des programmes.
Méthode peu coûteuse
Défauts:
-
Panels audimétriques
Des appareils enregistreurs (audimètres) sont placés dans les foyers
qui participent au panel.
Ils enregistrent le fonctionnement du récepteur et envoient
automatiquement l'information par voie téléphonique au milieu de la nuit.
Avantages:
Inconvénient:
ne mesurent que le fonctionnement du récepteur, sans tenir compte des
auditeurs
Solutions:
Difficultés générales
Questions non résolues
-
Faut-il compter toutes les personnes présentes dans la pièce ou
essayer de déterminer lesquelles regardent effectivement la TV ?
-
Quelle doit être la durée minimale d'écoute pour considérer
qu'un programme est suivi ?
-
Comment procéder lorsque les panélistes sont absents pour de longues
périodes (vacances,...)?
Les solutions adoptées varient d'un pays à l'autre.
Chapitre:
1
2
3
4
5
6
7
|





