|
L'histogramme et le polygone des effectifs donnent une vue globale et
détaillée de la distribution des individus dans un échantillon ou une
population.
Il est souvent très utile d'extraire de cette information des grandeurs
numériques qui en résument les caractéristiques essentielles.
Nous passerons tout d'abord en revue les grandeurs mesurant le
centre de la
distribution.
Ensuite, nous considérerons les différentes mesures de
l'étalement ou
dispersion de la distribution.
1. Centre d'une distribution
Il correspond au sommet de la distribution
|
Le mode est la valeur la plus fréquente
|
|
c'est la valeur la plus «à la mode»
On appelle distribution unimodale une
distribution présentant un seul mode
Une distribution bimodale est une
distribution présentant deux modes
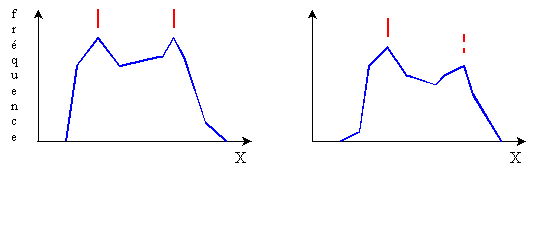
Une distribution multimodale est une
distribution présentant plusieurs modes
(2,3,...). Elle est souvent le reflet d'une population composée de
plusieurs sous-populations distinctes.
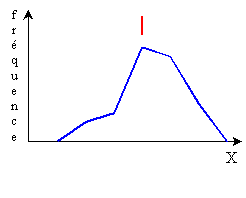
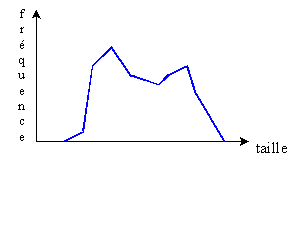
Par exemple, le polygone des fréquences ci-dessous, qui représente la
distribution de la taille des individus dans une population adulte,
présente deux modes. Ceux-ci sont le reflet de la présence de deux
sous-populations: les femmes et
les hommes, ces derniers étant généralement
plus grands.
Elle correspond au milieu de la distribution
|
la médiane est la valeur pour laquelle il y
a autant d'individus à gauche qu'à droite dans l'échantillon
|
|
Pour déterminer la médiane d'un échantillon ou d'une population:
(1) on classe les individus par ordre croissant;
(2) on prend celui du milieu
Exemple:
-
Soit un échantillon de 9 personnes dont le poids est:
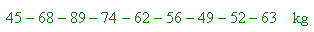
classés par ordre croissant:
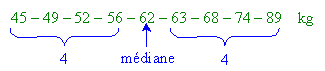
-
Si le nombre d'individus est pair, on prend la moyenne entre les deux
valeurs centrales:
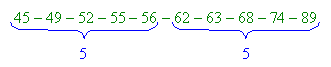
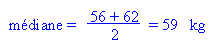
En règle générale, si n est le nombre
d'individus dans l'échantillon, la médiane porte le numéro d'ordre
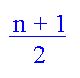
dans la suite des individus classés par ordre croissant.
Lorsqu'on obtient un numéro demi entier (ex: 24,5), on calcule la moyenne
des deux valeurs adjacentes.
Calcul de la médiane pour les grands
échantillons répartis en classes
-
Déterminez le numéro d'ordre de la médiane
-
Déterminez dans quelle classe elle se situe à l'aide du tableau des
nombres cumulés
-
Rangez par ordre croissant les éléments (individus) de cette classe
-
Sélectionnez l'élément (individu) correspondant au numéro choisi
Exemple:
Soient les pourcentages obtenus par 49 élèves à un examen, rangés par
classes de 10 pourcents de large
|
Classe
1-10
11-20
21-30
31-40
41-50
51-60
61-70
71-80
81-90
|
Nombre
2
4
5
8
7
9
6
6
2
|
Nombre cumulé
2
6
11
19
26
35
41
47
49
|
49 individus 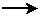 la médiane porte le n°25 la médiane porte le n°25
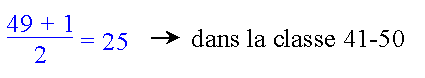
car, d'après le tableau des nombres cumulés, cette classe contient les
individus portant les numéros d'ordre 20 à 26.
Examinons le contenu de cette classe:
46 - 42 - 45 - 44 - 50 - 43 - 49
Rangeons-les par ordre croissant:
42 - 43 - 44 - 45 - 46 - 49 - 50
Il y a 19 individus dans les classes précédentes
 Le premier de cette classe
porte le n°20 et nous devons choisir le 25e Le premier de cette classe
porte le n°20 et nous devons choisir le 25e
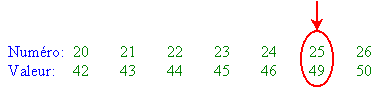
La médiane vaut donc 49
Elle correspond à une répartition "équitable"
de la grandeur mesurée sur tous les individus
|
la moyenne est la somme des grandeurs mesurées
divisée par le nombre d'individus
|
|
La moyenne d'une grandeur X est généralement notée
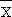
Exemple:
-
Dans le précédent échantillon de 9 personnes, le poids moyen vaut:
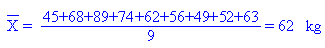
-
Dans le second échantillon de 10 personnes, le poids moyen vaut:
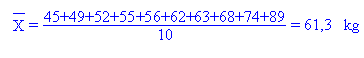
Pour un échantillon de n individus, la
moyenne est calculée par:
En utilisant la lettre grecque  pour représenter une somme, on obtient la notation compacte suivante:
pour représenter une somme, on obtient la notation compacte suivante:
Pour des données groupées en classes, on peut calculer une valeur
approximative de la moyenne en supposant que tous les individus d'une
classe se situent au centre de celle-ci.
Dans l'exemple précédent (9 personnes), la répartition est la suivante:
|
Classe
45-55
55-65
65-75
75-85
85-95
|
Centre
50
60
70
80
90
|
Nombre
3
3
2
0
1
|
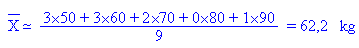
Si x est le centre de la classe et
f le nombre d'individus dans celle-ci,
la formule approchée s'écrit:
Dans l'exemple précédent, la formule approchée donne un poids moyen de
62,2 kg au lieu de
62 kg.
La formule approchée donnera des résultats d'autant meilleurs que:
|
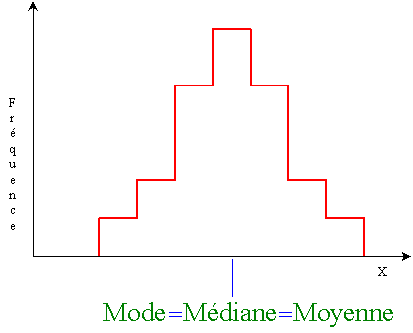
1.4. Positions relatives des trois mesures du centre d'une distribution
|
Distribution unimodale et symétrique
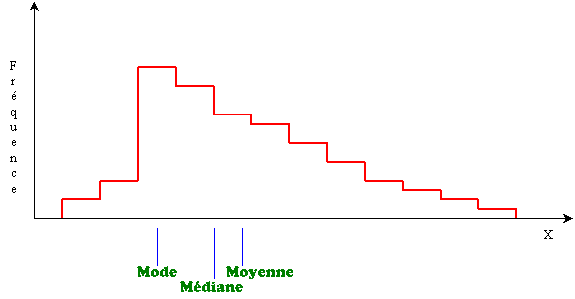
Distribution asymétrique
A. Distribution étalée é droite:
B. Distribution étalée é gauche:
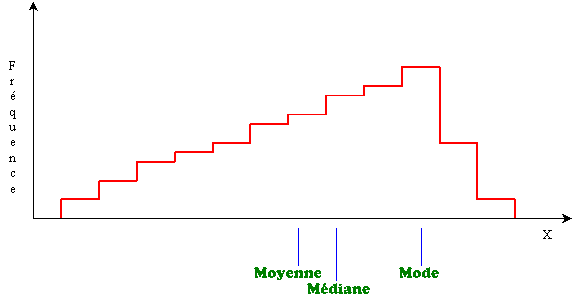
|
1.5. Qualité comparée des trois mesures du centre d'une distribution
|
Exemple:
Répartition des revenus dans une population.
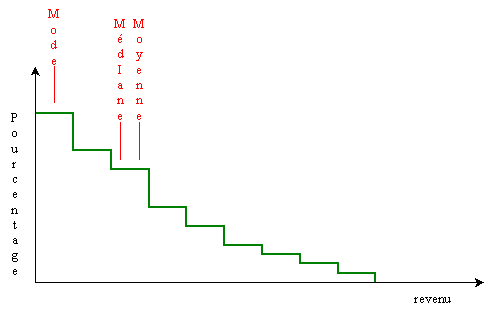
Le mode est la plus mauvaise mesure du
centre, car la classe la mieux représentée n'est pas nécessairement au
centre de la distribution.
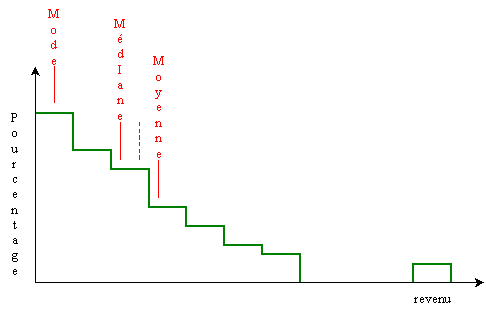
Si les valeurs entrêmes sont modifiées, la
médiane ne change pas car elle n'est pas sensible aux valeurs
extrêmes. Par contre la moyenne change
car elle tient compte de toutes les valeurs.
On préferera la
médiane ou la
moyenne selon que l'on veut une mesure sensible ou non aux valeurs
extrêmes.
2. Etalement d'une distribution
|
2.1. Dispersion d'une distribution
|
Supposez que l'on désire comparer les revenus des ouvriers d'une usine à
ceux de l'ensemble de la population de leur région.
Les résultats sont résumés sur l'histogramme suivant:
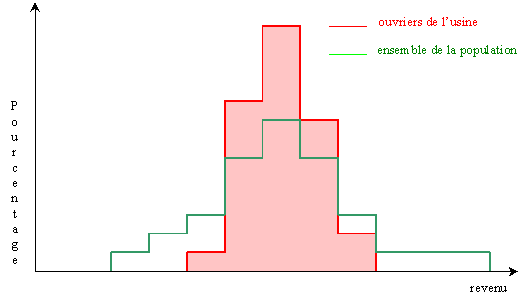
Dans ce cas, les deux distributions ont le même centre mais elles
sont manifestement différentes:
elles diffèrent par leur dispersion
Mesures de la dispersion
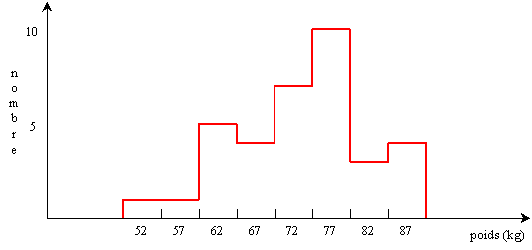
Exemple:
Les poids de 35 garçons de 2e candi. communication (97-98) sont
repris dans le tableau et l'histogramme suivants:
|
classe (kg)
|
individus: poids en kg
| 50-54 |
52
| 55-59 |
58
| 60-64 |
62 60 60 63 62
| 65-69 |
65 65 66 65
| 70-74 |
72 70 72 74 74 74 70
| 75-79 |
75 75 75 75 76 75 75 75 75 78
| 80-84 |
80 80 80
| 85-89 |
89 88 88 87
|
Pour caractériser l'étendue d'une distribution, les statisticiens ont
introduit toute une série de grandeurs, dont nous allons considérer les
principales.
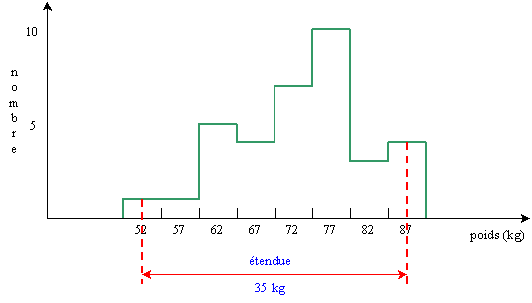
L'étendue est la
différence entre la
plus grande valeur et la
plus petite valeur.
Dans l'exemple précédent, le calcul exact donne:
89 - 52 = 37 kg
Un calcul approché, prenant en compte le centre des classes, donnerait:
87 - 52 = 35 kg
|
2.3. L'étendue interquartile
|
Le premier quartile est l'individu ayant
25 % de l'échantillon en-dessous de lui
et 75 % de l'échantillon au-dessus.
Le deuxième quartile est l'individu ayant
50 % de l'échantillon en-dessous de lui
et 50 % de l'échantillon au-dessus.
(c'est donc la médiane)
Le troisième quartile est l'individu ayant
75 % de l'échantillon en-dessous de lui
et 25 % de l'échantillon au-dessus.
|
L'étendue interquartile est la différence entre le
troisième et le premier quartiles
|
|
Dans notre exemple, on a:
1er quartile = 65 kg
2me quartile = 76 kg
Etendue interquartile
(EIQ) = 76-65 = 11 kg
n°
|
|
poids (kg)
|
| |
1
2
3
4
5
6
7
8 |
52
58
60
60
62
62
63
65 | |
9 |
 | 65 |
1er quartile |
 |
10
11
12
13
14
15
16
17 | |
65
66
70
70
72
72
74
74 | | |
18 |  |
74 |
médiane |
 EIQ:
76-65 = 11 kg EIQ:
76-65 = 11 kg
|
19
20
21
22
23
24
25
26 | |
75
75
75
75
75
75
75
75 | | |
27 |  |
76 |
3ème quartile |
 |
28
29
30
31
32
33
34
35 | |
78
80
80
80
87
88
88
89 | | |
|
2.4. L'écart absolu moyen
|
On désire une quantité qui mesure l'écart
moyen par rapport à la moyenne.
On ne peut pas simplement calculer la moyenne des écarts, car celle-ci est
toujours nulle.
Exemple:
Soient les 5 valeurs suivantes:
4, 6, 9, 10, 11
La moyenne vaut: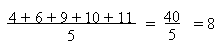
valeur |
écart à la moyenne |
4
6
9
10
11 |
4-8 = -4
6-8 = -2
9-8 = 1
10-8 = 2
11-8 = 3 |
moyenne des écarts: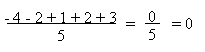
Ce résultat est toujours valable, il résulte
de la définition de la moyenne.
L'écart absolu moyen est la moyenne
des écarts par rapport à la moyenne, toujours comptés positifs.
C'est donc la moyenne des valeurs
absolues des écarts à la moyenne.
Dans le dernier exemple, il vaut:
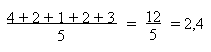
|
2.5. L'écart quadratique moyen
|
Pour des raisons mathématiques, il est préférable, pour éliminer les
signes
-, de calculer le carré des écarts
plutôt que leur valeur absolue.
On calcule donc la moyenne des
carrés des écarts, puis on en prend la
racine carrée:
Dans l'exemple ci-dessus, on a:
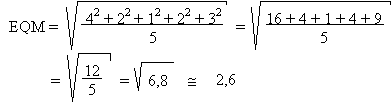
Toujours pour des raisons mathématiques, il est préférable, de diviser
par n-1 plutôt que par
n pour estimer précisément la dispersion
d'une population à partir d'un
échantillon.
On obtient alors l'écart type, qui est
préférable à l'écart quadratique moyen, et l'on retiendra seulement
la formule suivante:
Dans l'exemple ci-dessus, on a:
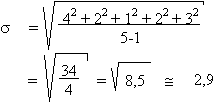
Pourquoi l'écart type est-il
préférable à l'écart quadratique moyen ?
Si on se contentait de décrire l'échantillon,
l'écart quadratique moyen serait une bonne mesure de la dispersion.
Mais, en général, nous sommes intéressés par la
population sous-jacente, dont l'échantillon
n'est qu'une partie (supposée représentative).
On veut donc estimer la moyenne et la dispersion de
la population à partir de l'échantillon.
Cas extrême:
Supposons que nous ne disposions que d'un échantillon de
1 individu.
On peut estimer le poids moyen de la population: ce sera le poids de
l'individu (ex.: 65 kg)
L'écart quadratique moyen donnerait une dispersion nulle, ce qui suggère
que toute la population pèse 65 kg !
L'écart type nous indique que nous ne pouvons pas estimer la dispersion
dans la population si notre échantillon ne comporte pas au moins
2 individus, (car on ne peut pas diviser par
zéro).
Calcul de l'écart type pour un échantillon réparti en classes
Soient: |
x
f
n |
les centres des classes
Les effectifs
la moyenne
de l'échantillon
le nombre total d'individu |
On peut calculer une valeur approchée de l'écart type en supposant que
tous les individus d'une classe sont au centre de celle-ci:
Chapitre:
1
2
3
4
5
6
7
|





